DiffHuman: Probabilistic Photorealistic 3D Reconstruction of Humans

CVPR 2024

¹Google Research, ²University of Cambridge

Abstract

We present DiffHuman, a probabilistic method for photorealistic 3D human reconstruction from a single RGB image. Despite the ill-posed nature of this problem, most methods are deterministic and output a single solution, often resulting in a lack of geometric detail and blurriness in unseen or uncertain regions. In contrast, DiffHuman predicts a probability distribution over 3D reconstructions conditioned on an input 2D image, which allows us to sample multiple detailed 3D avatars that are consistent with the image. DiffHuman is implemented as a conditional diffusion model that denoises pixel-aligned 2D observations of an underlying 3D shape representation. During inference, we may sample 3D avatars by iteratively denoising 2D renders of the predicted 3D representation. Furthermore, we introduce a generator neural network that approximates rendering with considerably reduced runtime (55x speed up), resulting in a novel dual-branch diffusion framework. Our experiments show that DiffHuman can produce diverse and detailed reconstructions for the parts of the person that are unseen or uncertain in the input image, while remaining competitive with the state-of-the-art when reconstructing visible surfaces.

Method

3D human avatars are represented as neural implicit surfaces \(\mathcal{S}\) - specifically as the zero-level-sets of signed distance fields (SDFs). We predict a distribution over 3D human surfaces \(p_\Theta (\mathcal{S} | \mathbf{I})\) conditioned on an input image \(\mathbf{I}\) using a denoising diffusion probabilistic model.

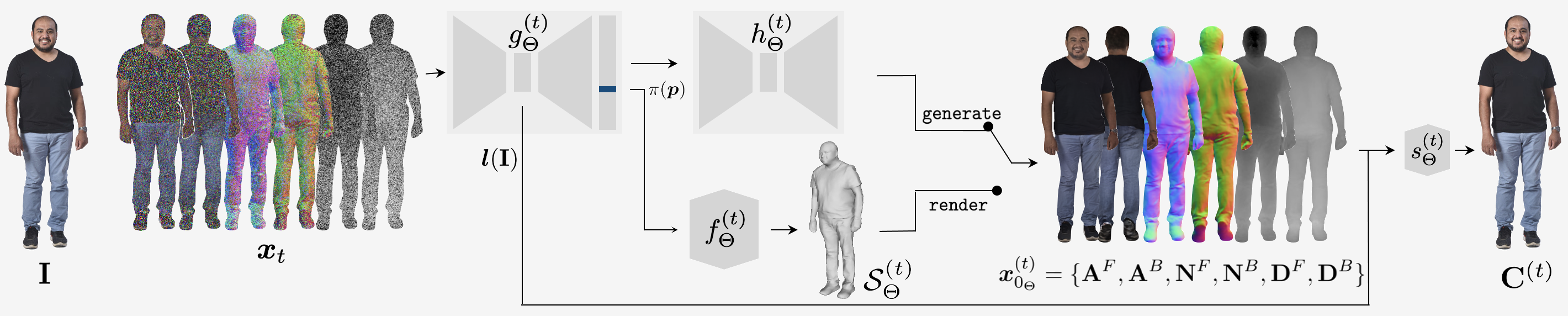
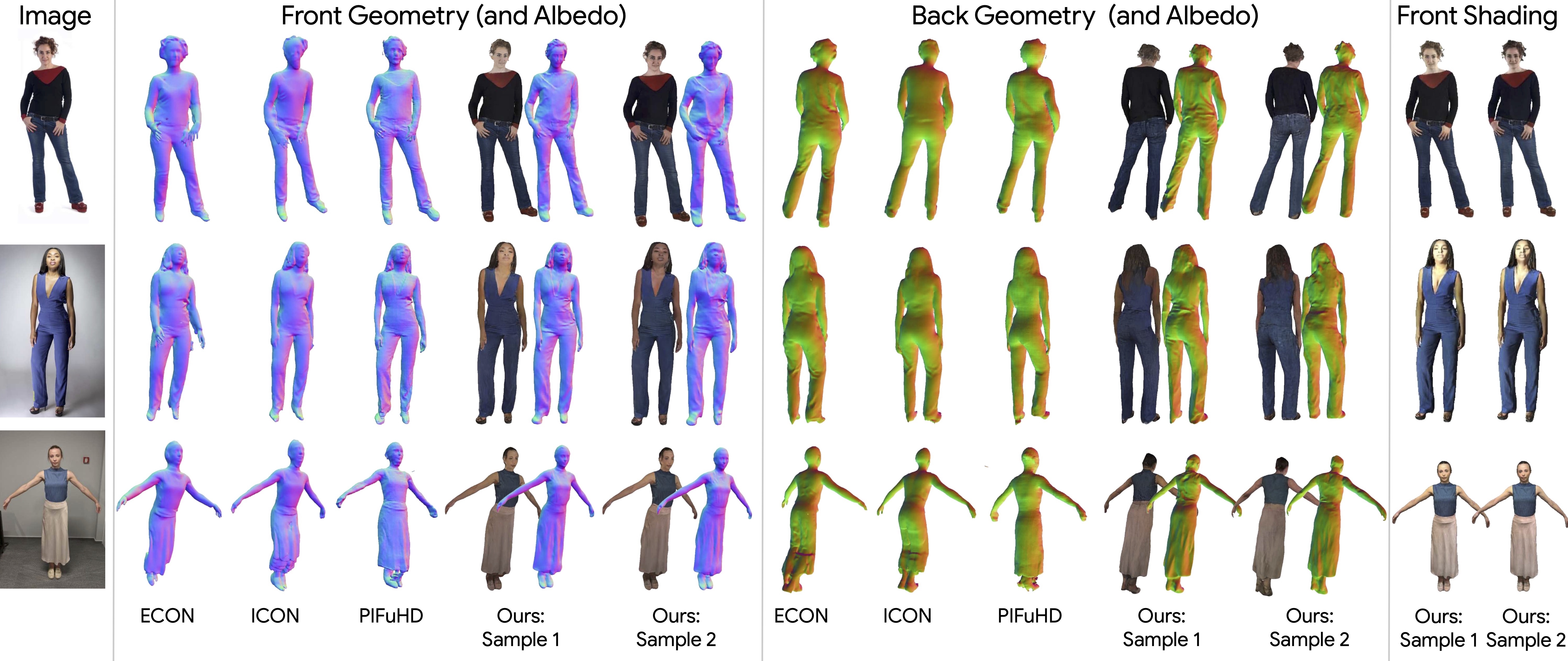
In practice, we model a distribution over image-based pixel-aligned observations of the surface \(\mathcal{S}\). Front and back albedo images, surface normal images and depth maps comprise an "observation set" \(\boldsymbol{x}_0 = \{\mathbf{A}^F, \mathbf{A}^B, \mathbf{N}^F, \mathbf{N}^B, \mathbf{D}^F, \mathbf{D}^B \}\). Since \(\boldsymbol{x}_0\) is effectively a multichannel image, we can borrow architectural components and methods from conventional image-based diffusion models.

Our denoising diffusion model outputs a prediction of the “clean” observation set \(\boldsymbol{x}_{0_\Theta}^{(t)}\) given a noisy version \(\boldsymbol{x}_t\). An underlying surface \(\mathcal{S}_\Theta^{(t)}\) is estimated as an intermediate 3D representation in each denoising step, given by the zero-level-set of an SDF \(f_\Theta^{(t)}\) conditioned on pixel-aligned features \(g_\Theta^{(t)} (\boldsymbol{x}_t, \mathbf{I})\). \(f^{(t)}_\Theta\) and \(g^{(t)}_\Theta\) are both neural networks. \(\boldsymbol{x}_{0_\Theta}^{(t)}\) is obtained by rendering \(\mathcal{S}_\Theta^{(t)}\).

During inference, we can sample trajectories over observation sets \(\boldsymbol{x}_{0:T} \sim p_\Theta(\boldsymbol{x}_{0:T} | \mathbf{I})\) by computing and rendering \(\mathcal{S}_\Theta^{(t)}\) in each denoising step. The final implicit surface \(\mathcal{S} = \mathcal{S}_\Theta^{(1)}(\boldsymbol{x}_1, \mathbf I)\) represents a 3D reconstruction sample \(\mathcal{S} \sim p_\Theta(\mathcal{S}| \mathbf{I})\).

However, computing and rendering a neural implicit surface in every denoising step is very computationally expensive. To alleviate this, we additionally train a "generator" neural network \(h_\Theta^{(t)}\) that directly maps features \(g_\Theta^{(t)} (\boldsymbol{x}_t, \mathbf{I})\) to \(\boldsymbol{x}_{0_\Theta}^{(t)}\) with an image-to-image architecture. During inference, we denoise using \(h_\Theta^{(t)}\), and only explicitly compute a 3D surface in the final denoising step. This results in a 55x speed-up over rendering in every step.

In addition, we can produce a shaded render of \(\mathcal{S}\) using a pixel-wise shading network \(s_\Theta^{(t)}\) that computes per-pixel RGB shading coefficients given the surface normal at that pixel, and an estimated scene illumination code \(\boldsymbol{l}(\mathbf{I})\). The shaded render \(\mathbf{C}^{(t)}\) matches the input image, and allows us to decouple surface albedo and shading.

Comparison against Deterministic Methods

(Hover to zoom)
This figure compares DiffHuman against PHORHUM and S3F. PHORHUM outputs excellent front predictions, but exhibits over-smooth, flat geometry and blurry colours on the back. S3F yields more detailed geometry, but colours are still often blurry. Moreover, both these methods occasionally paste the front colour predictions onto the back incorrectly (see row 3). Samples from DiffHuman achieve a greater level of geometric detail and colour sharpness in uncertain regions.

Comparison against deterministic methods that estimate only geometry.

(Hover to zoom)
Here we compare DiffHuman against PIFuHD, ICON and ECON. These deterministic methods often fall back towards the mean of the training data distribution when faced with ambiguous and challenging inputs; e.g. predicting trousers from the back instead of a long skirt in row 3. This can be mitigated by predicting distributions over reconstructions instead, thus modelling the inherent ambiguity in this task.

Denoising Trajectory and Diversity Visualisation

This visualises the denoising trajectory for a single sample, showing the noisy observation set \(\boldsymbol{x}_t\) and clean prediction \(\boldsymbol{x}^{(t)}_{0_\Theta}\) at each timestep. \(\boldsymbol{x}^{(t)}_{0_\Theta}\) is initially simple (see back normals); geometric and colour-wise details develop over the reverse process.

We can show the emergence of sample diversity over the reverse process using the per-pixel variance of the observations in \(\boldsymbol{x}^{(t)}_{0_\Theta}\) at each timestep. Blue indicates a lower variance and red indicates a higher variance, computed over 10 samples. \(\boldsymbol{x}^{(t)}_{0_\Theta}\) becomes more diverse over time as the samples diverge. The back surface is, intuitively, more uncertain than the front.

Unconditional and Edge-Conditioned Samples

We can obtain unconditional samples from DiffHuman by training a model with random condition dropping. These samples are generated from random noise only, which is masked using a silhouette in the shape of the desired subject. However, faces and other details within the silhouette may be blurry, due to a lack of conditioning signal.

(Hover to zoom)
Conditioning on edge-maps enables finer control than masked random noise, e.g. over in-silhouette details such as facial features and clothing boundaries. These samples are generated using a DiffHuman model that was pre-trained with conditioning RGB images, and then fine-tuned using conditioning edge maps. This demonstrates that samples from DiffHuman can be controlled via simpler conditioning inputs than full RGB images, which opens the possibility for generative applications beyond reconstruction.

BibTeX

@inproceedings{ sengupta2024diffhuman, author = {Sengupta, Akash and Alldieck, Thiemo and Kolotouros, Nikos and Corona, Enric and Zanfir, Andrei and Sminchisescu, Cristian}, title = {{DiffHuman: Probabilistic Photorealistic 3D Reconstruction of Humans}}, booktitle = {CVPR}, month = {June}, year = {2024} }

DiffHuman: Probabilistic Photorealistic 3D Reconstruction of Humans

CVPR 2024

Monocular 3D human reconstruction is an ill-posed problem - multiple 3D solutions can explain a single 2D image, due to depth ambiguity, (self-)occlusion and unseen body parts. DiffHuman predicts a probability distribution over photorealistic 3D reconstructions conditioned on a single RGB image.

We can sample several plausible, diverse and input-consistent reconstructions during inference, in contrast to deterministic approaches^[1,2] that output a single estimate.

Samples from DiffHuman exhibit a greater level of geometric and colour-wise detail than deterministic methods^[1,2], particularly in unseen and uncertain regions of the human body such as the back-side.

Samples from DiffHuman exhibit a greater level of geometric and colour-wise detail than deterministic methods^[1,2], particularly in unseen and uncertain regions of the human body such as the back-side.

Abstract

Video Overview

Method

Results

Comparison against Deterministic Methods

Denoising Trajectory and Diversity Visualisation

Unconditional and Edge-Conditioned Samples

BibTeX

DiffHuman: Probabilistic Photorealistic 3D Reconstruction of Humans

CVPR 2024

Monocular 3D human reconstruction is an ill-posed problem - multiple 3D solutions can explain a single 2D image, due to depth ambiguity, (self-)occlusion and unseen body parts. DiffHuman predicts a probability distribution over photorealistic 3D reconstructions conditioned on a single RGB image.

We can sample several plausible, diverse and input-consistent reconstructions during inference, in contrast to deterministic approaches[1,2] that output a single estimate.

Samples from DiffHuman exhibit a greater level of geometric and colour-wise detail than deterministic methods[1,2], particularly in unseen and uncertain regions of the human body such as the back-side.

Samples from DiffHuman exhibit a greater level of geometric and colour-wise detail than deterministic methods[1,2], particularly in unseen and uncertain regions of the human body such as the back-side.

Abstract

Video Overview

Method

Results

Comparison against Deterministic Methods

Denoising Trajectory and Diversity Visualisation

Unconditional and Edge-Conditioned Samples

BibTeX

We can sample several plausible, diverse and input-consistent reconstructions during inference, in contrast to deterministic approaches^[1,2] that output a single estimate.

Samples from DiffHuman exhibit a greater level of geometric and colour-wise detail than deterministic methods^[1,2], particularly in unseen and uncertain regions of the human body such as the back-side.

Samples from DiffHuman exhibit a greater level of geometric and colour-wise detail than deterministic methods^[1,2], particularly in unseen and uncertain regions of the human body such as the back-side.